Miscellaneous drills on addition
Mastering Input-Output Math Drills: Strategies and Tips
Welcome to Clever Calc! Today, we’ll explore the fascinating world of input-output math drills. These exercises help students understand functional relationships and the rules that connect inputs to outputs. We'll provide examples, explain methods for solving these problems, and offer tips for teachers to enhance their instruction.
Understanding Input-Output Math Drills
Input-output tables present a set of input numbers and corresponding output numbers based on a specific rule. The challenge for students is to determine the rule and use it to find missing values.
Example Problems and Solutions
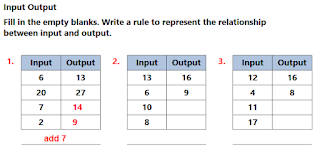
Example 1:
Input: 6, 20, 7, 2
Output: 13, 27, 14, 9
Rule: Add 7
Steps to Solve:
- Identify the relationship: Look at the input and output pairs to find a consistent change.
- 6 → 13 (13 - 6 = 7)
- 20 → 27 (27 - 20 = 7)
- 7 → 14 (14 - 7 = 7)
- 2 → 9 (9 - 2 = 7)
- Formulate the rule: The rule here is to add 7 to each input to get the output.
- Apply the rule: Fill in missing values using the rule.
Example 2:
Input: 13, 6, 10, 8
Output: 16, 9, ___, ___
Rule: Add 3
Steps to Solve:
- Identify the relationship:
- 13 → 16 (16 - 13 = 3)
- 6 → 9 (9 - 6 = 3)
- Formulate the rule: The rule is to add 3 to each input to get the output.
- Apply the rule:
- 10 + 3 = 13
- 8 + 3 = 11
- Fill in the blanks: 10 → 13 and 8 → 11
Example 3:
Input: 12, 4, 11, ___
Output: 16, 8, ___, ___
Rule: Add 4
Steps to Solve:
- Identify the relationship:
- 12 → 16 (16 - 12 = 4)
- 4 → 8 (8 - 4 = 4)
- Formulate the rule: The rule is to add 4 to each input to get the output.
- Apply the rule:
- 11 + 4 = 15
- 17 + 4 = 21
- Fill in the blanks: 11 → 15 and 17 → 21
Teaching Tips for Educators
- Introduce the Concept Gradually:
- Start with simple rules (e.g., add 2, subtract 1) before moving to more complex operations.
- Ensure students understand basic arithmetic operations as these are foundational.
- Use Visual Aids:
- Utilize charts, tables, and number lines to visually represent the relationships.
- Color-code inputs and outputs to make patterns more noticeable.
- Encourage Pattern Recognition:
- Ask students to describe the pattern they see before writing the rule.
- Use multiple examples to show consistent patterns and rules.
- Interactive Activities:
- Incorporate games and group activities where students create their own input-output tables.
- Use manipulatives like counters or blocks to physically represent the changes.
- Real-World Connections:
- Relate input-output problems to real-life scenarios (e.g., recipes, shopping lists) to make learning more relevant.
- Discuss how functions and rules apply to everyday activities.
- Provide Step-by-Step Practice:
- Offer guided practice with immediate feedback to build confidence.
- Gradually increase the difficulty level as students become more proficient.
Conclusion
Input-output math drills are a powerful tool for developing students' understanding of mathematical relationships and functions. By identifying and applying rules, students enhance their problem-solving skills and gain a deeper appreciation for math. Teachers can use the strategies outlined here to create engaging and effective lessons that support student learning.
Understanding the Addition Box Puzzle: A Step-by-Step Guide
Puzzles are a great way to stimulate the mind and enhance problem-solving skills. One interesting type of puzzle is the addition box puzzle. In this blog post, we'll explore how to solve an addition box puzzle using a specific example. Let's dive in!
The Puzzle Layout
The puzzle consists of a 3x3 grid filled with numbers, along with several additional boxes surrounding it. Here's the grid and the associated boxes:
Our task is to understand the relationship between the numbers in the grid and the numbers in the surrounding boxes.
Step-by-Step Solution
To solve this puzzle, we need to examine the sums of the numbers in the grid and compare them to the numbers in the surrounding boxes.
1. Sum of Rows
First, let's calculate the sum of the numbers in each row:
- First row: 7 + 7 + 14 = 28
- Second row: 18 + 2 + 8 = 28
- Third row: 12 + 7 + 13 = 32
The numbers in the rightmost column (28, 28, 32) correspond to the sums of the rows from top to bottom.
2. Sum of Columns
Next, let's calculate the sum of the numbers in each column:
- First column: 7 + 18 + 12 = 37
- Second column: 7 + 2 + 7 = 16
- Third column: 14 + 8 + 13 = 35
The numbers in the bottom row (37, 16, 35) correspond to the sums of the columns from left to right.
3. Sum of Diagonals
Now, let's calculate the sums of the numbers in the diagonals:
- First diagonal (from top left to bottom right): 7 + 2 + 13 = 22
- Second diagonal (from top right to bottom left): 14 + 2 + 12 = 28
The numbers 22 and 28 correspond to these diagonal sums.
Conclusion
By examining the sums of the rows, columns, and diagonals, we can understand the pattern in the addition box puzzle. The surrounding numbers provide a summary of these sums:
- The numbers on the right (28, 28, 32) represent the sums of the rows.
- The numbers at the bottom (37, 16, 35) represent the sums of the columns.
- The numbers 22 and 28 represent the sums of the diagonals.
This method can be applied to similar puzzles, making it easier to decipher the relationships and solve the puzzle efficiently. Happy puzzling!
Stay tuned to Clever Calc for more insightful tips, resources, and activities to make math both engaging and enjoyable!




Post a Comment
0 Comments